- Eufrasia Caela V.M. / 13
- Irene Tedjasukmana / 17
- Joanna Jedine S. / 21
- Mary Catherine W. / 28
1. Diketahui kubus ABCD.EFGH dengan panjang rusuk 12 cm. Hitunglah besar sudut antara garis AH dan EG !
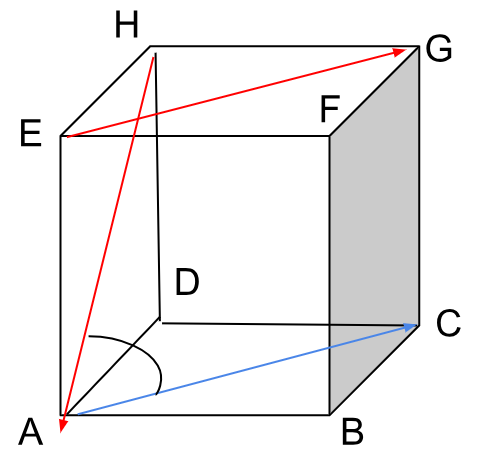
Garis proyeksi EG adalah AC
Sudut antara AH dan EG = AH dan AC
AH = √DH² + AD²
= √12² + 12²
= √288
= 12√2
AH = HC = AC = diagonal sisi = 12√2
Maka, besar sudut antara garis AH dan EG adalah 180°/3 = 60°
2. Diketahui kubus ABCD.EFGH dengan rusuk 8 cm. M adalah titik tengah EH. Hitunglah jarak titik M ke AG !
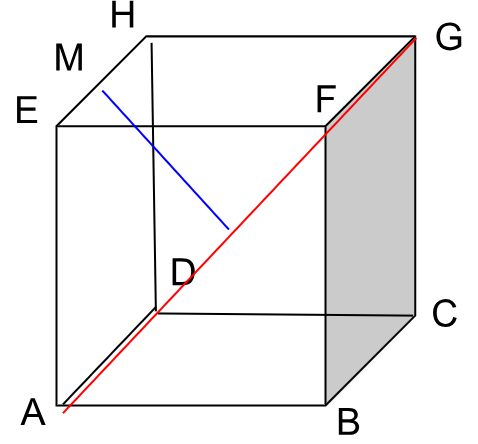
MG = AM = 1/2 . 8 . √5 = 4√5
AG = 8√3
Tinggi segitiga AGM = √MG² – (12AG)²
= √(45)²-(43)²
= √80-48
= √32
= 4√2 cm
3. Diketahui kubus ABCD.EFGH dengan panjang rusuk 3 cm. Jarak titik C ke bidang BDG adalah…
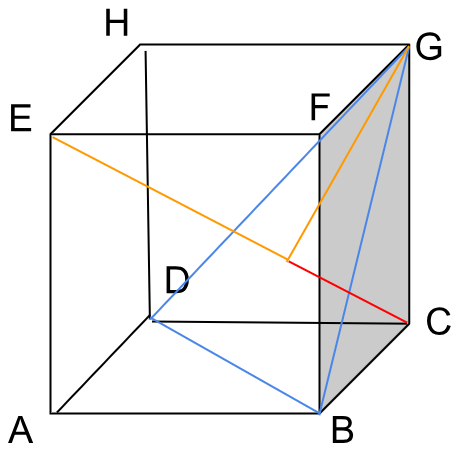
(Cara cepat)
Panjang diagonal ruang = 3√3 cm.
Jarak titik C ke bidang BD
= 1/3 dari panjang diagonal ruang.
= 1/3 . 3√3 cm
= √3 cm
4. Jika luas bidang diagonal suatu kubus adalah 36√2 cm2, panjang diagonal ruang kubus adalah…
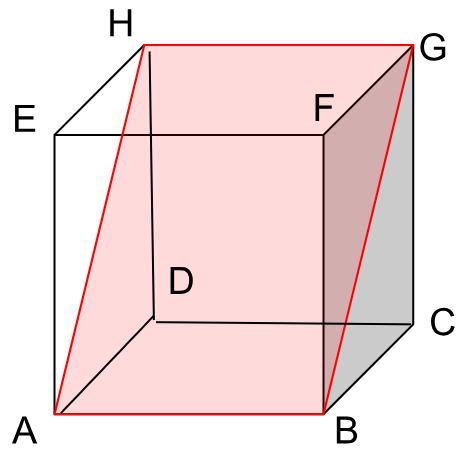
Luas bidang diagonal kubus = diagonal bidang × rusuk
36√2 = a√2.a
36√2 = a2√2
36 = a2
6 = a
Diagonal ruang adalah a√3 = 6√3 cm
5. Diketahui kubus ABCD.EFGH dengan panjang rusuk 6 cm. Jarak titik F ke tengah garis AB adalah …
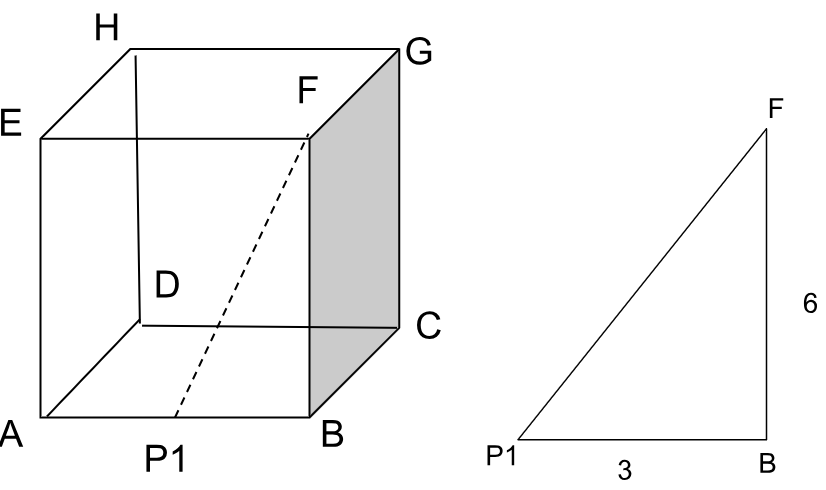
x = √6²+3²
= √36 + 9
= √45
= √9 x 5
= 3√5 cm
6. Diketahui kubus ABCD.EFGH dengan panjang rusuk 10 cm. Cosinus sudut antara garis GC dan bidang BDG adalah ….
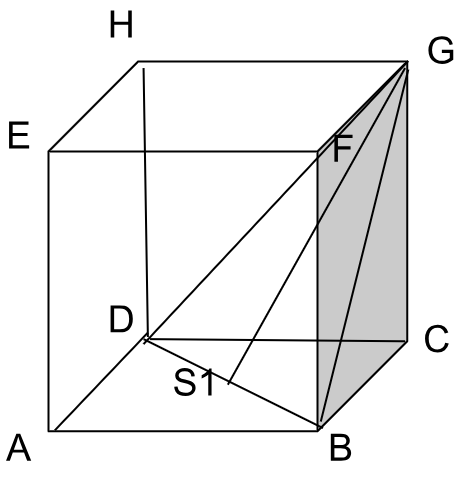
cos ⍺ = CG/PG
= 10/8√6
= 2/√6 . √6/√6
= 2/6√6
CS1 = 1/2 . AC
= 1/2 . a√2
= 1/2 . 10√2 = 5√2
GS1 = √CS1² + CG²
= √(5√2)² + 10²
= √25 . 2 + 100
= √50 + 100
= √150
= √25 . 6
= 5√6 cm
7. Jika kubus di bawah memiliki panjang rusuk 6 cm, dan titik x merupakan titik ditengah-tengah AB, maka tentukanlah titik H ke titik A!
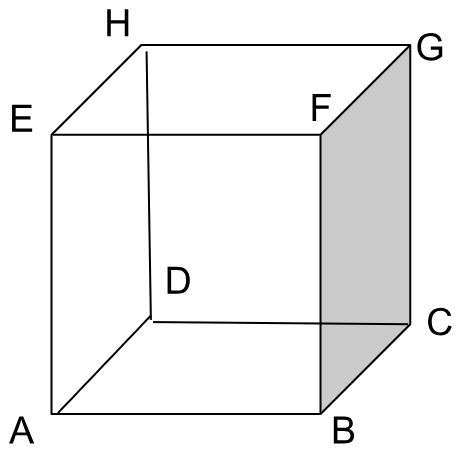
HA = √HE² + EA²
HA = √(6²+6²)
HA = √(36+36)
HA = √72
HA = 6√2 cm
8. Diketahui kubus ABCD. EFGH dengan panjang rusuk 8 cm. hitunglah jarak garis AE ke bidang BDHF?
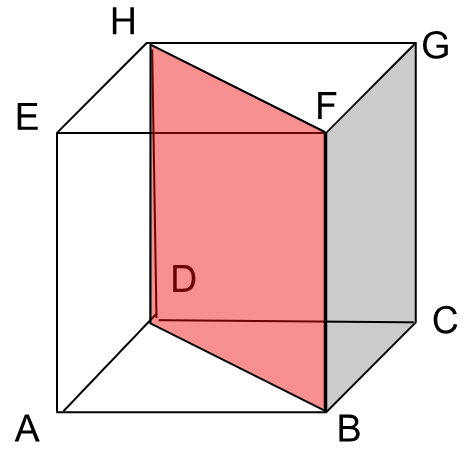
AP = 1/2 AC(AC ⊥ BDHF)
= 1/2 . 8√2
= 4√2 cm
