(Audy/02, Calista/05, Evelyn/14, Ozora/31)
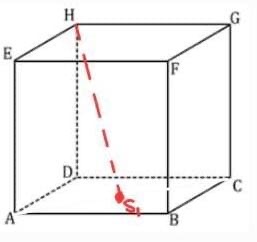
1.H pada AC = S1
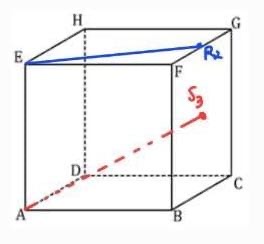
2. AS3 pada EFGH = ER2
ER3 = √(EF^2 + FR^2)
ER3 = √(a^2 +(1/2a)^2)
ER3 = √(5/4a^2)
ER3 = 1/2a√5
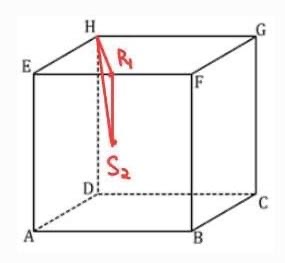
3. HS2 = √(HR1^2 + R1S2^2)
HS2 = √((1/2a√5)^2 + (1/2a)^2)
HS2 = √(6/4a^2)
HS2 = 1/2a√6
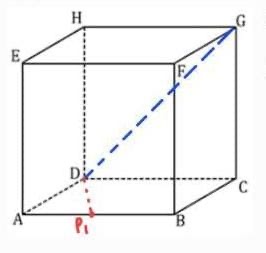
4. P1 ke DG = P1D
P1D= √(DA^2 + A1^2)
P1D= √a^2 + (1/2a)^2
P1D= 1/2a√(5)
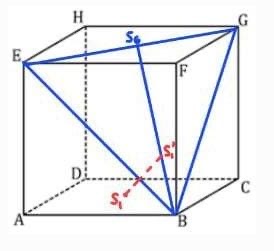
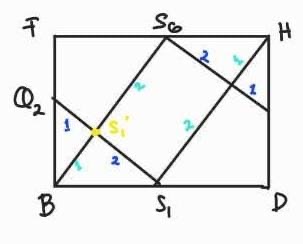
5. S1 ke BEG = S1 ke BS6
Karena S1 dan BS6 terletak pada bidang BDHF, maka
Jarak S1 ke BS6 = S1S1′
S1S1′ = 2/3S1Q2 S1S1′ = 2/3√(BQ2^2 + BS1^2)
S1S1′ = 2/3√((1/2a)^2 + (1/2a√2)^2) S1S1′ = 2/3√(3/4a^2)
S1S1′ = 2/3*1/2a√3
S1S1′ = 1/3a√3
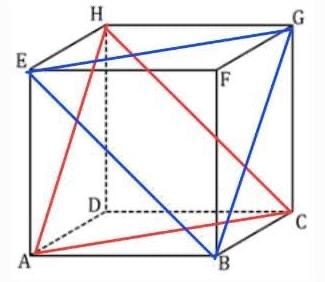
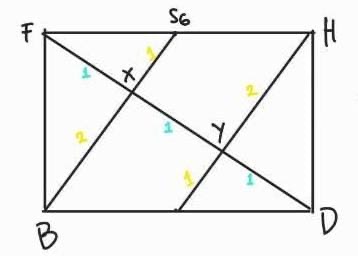
6. ACH — BEG dapat diwakili oleh garis (HS1) = (BS6)
Maka jarak HS1 & BS6 = XY
XY = 1/3*DF = 1/3a√3
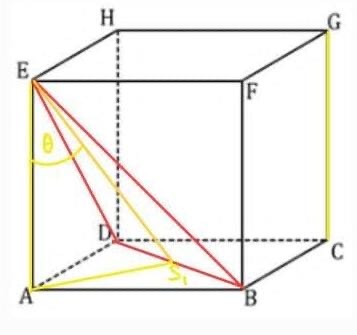
7. sin (CG, BDE) = sin (AE, ES1)
- AE sebagai Perwakilan CG, karena AE //CG
- ES1, Sebagai perwakilan ABDE Pada Segitiga EAS, diketabui bahwa siku-siku di A, sehingga:
sin theta = de/mi
sin theta = (AS1/ES1)
sin theta = (1/2a√2))/(1/2a√6) = 1/3*√3
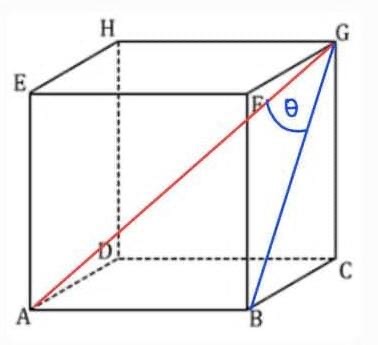
8. cos (AG,BCGF) = cos (AG, BG)
Karena AB tegak lurus BG maka segitiga ABG siku” di B, sehingga
cos theta = (Sa)/(mi)
cos theta = (BG)/(AG) = (1/2a√2)/(1/2a√3) = 1/3√6
