Oleh: Caithlyn Lijanto XII IPS 1/04, Elisabeth Florentina Zhuputri XII IPS 1/11, Fanelynn Fay Teonata XII IPS 1/15, Isabella Kimberly Yauwerisa XII IPS 1/18
1. Penyelesaian:
Berdasarkan gambar di atas, titik S diproyeksikan terhadap garis CD hingga terbentuk titik S’. Sementara itu, jarak antara titik S ke garis CD sama dengan panjang garis SS’. Oleh karena garis SS’ sejajar dengan rusuk kubus ABCD.EFGH, maka panjang SS’ = panjang rusuk kubus ABCD.EFGH = 8 cm.
Jadi, jarak antara titik S ke garis CD adalah 8 cm.
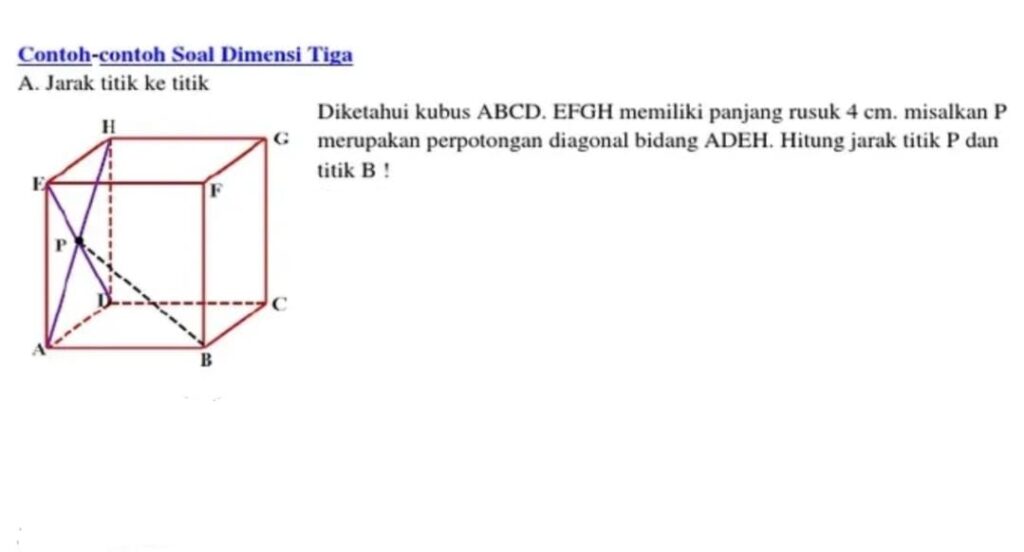
2. Penyelesaian
AH=√(AE)²+(EH)² = √(4²+4²
= √32
AH =4√2
AP=½ ×AH =½ ×4√2
=2√2
Jadi, jarak titik B ke titik P adalah panjang BP:
BP=(AB)²+(AP)²=4²+(2√2)²
=√16+8 = √24 = 2√6
Jadi, jarak titik B ke perpotongan bidang ADEH adalah 2√6.
Diketahui kubus ABCDEFGH dengan panjang rusuk 8 cm, Hitunglah jarak antara Titik C ke E
3. Penyelesaian
Jarak Titik C ke E
AC = AF = Diagonal Sisi
= a√2
= 8√2
(CE)² = (AE)² + (AC)²
= (8)²+(8√2)²
= 64 + 128
= 192
CE =√192
= √64 x 3
= 8√3
Diketahui kubus PQRSTUV dengan panjang rusuk 6 cm, Hitunglah jarak antara Titik X ke V
4. Penyelesaian
Jarak Titik X ke V
QV = Diagonal Sisi
= a√2
= 6√2
(XV)² = (XQ)²+(QV)²
(XV)² = (3)2+(6√2)2
(XV)² = 9 + 72
(XV)² = 81
XV = √81
XV = 9 cm
Jika kubus di bawah ini memiliki panjang rusuk 6cm, dan titik X merupakan titik di tengah – tengah AB, maka tentukanlah titik H ke titik A!
5. Penyelesaian
HA = √HE² + EA²)
HA = √(6²+6²)
HA = √(36+36)
HA = √72
HA = 6√2 cm
Diketahui kubus ABCD.EFGH dengan panjang rusuk 8 cm. Jarak titik H ke garis AC adalah…
6. Penyelesaian
arak titik H ke garis AC adalah OH.
Rusuk = a = 8
OH = a/2√6 = 8/2√6 = 4√6
Tentukan jarak antara titik E ke diagonal BD pada kubus dengan panjang sisi 20 cm!
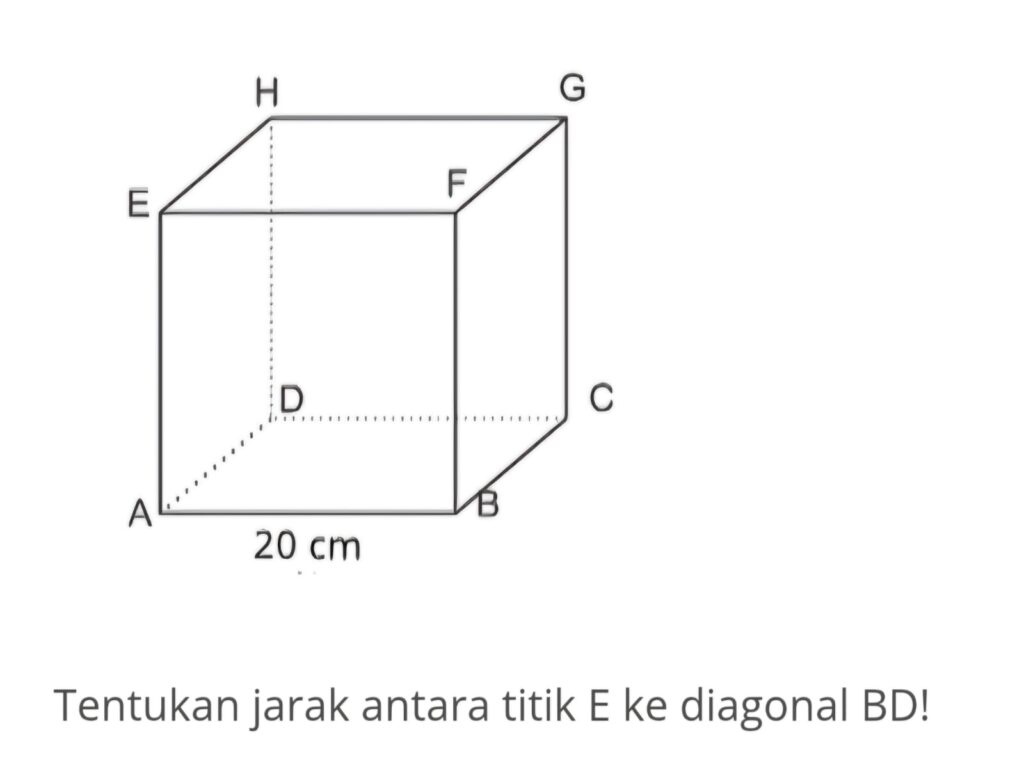
7. Penyelesaian
Jawaban:
Langkah 1: Menentukan Titik Tengah Diagonal BD
AQ = (1/2) × AC
AQ = (1/2) × (20√2)
AQ = 10√2 cm
Langkah 2: Menggunakan Teorema Pythagoras untuk Mencari EQ
EQ = √(AQ² + EA²)
EQ = √((10√2)² + 20²)
EQ = √(200 + 400)
EQ = √600
EQ = 10√6 cm
Jadi, jarak antara titik E ke diagonal BD adalah 10√6 cm.
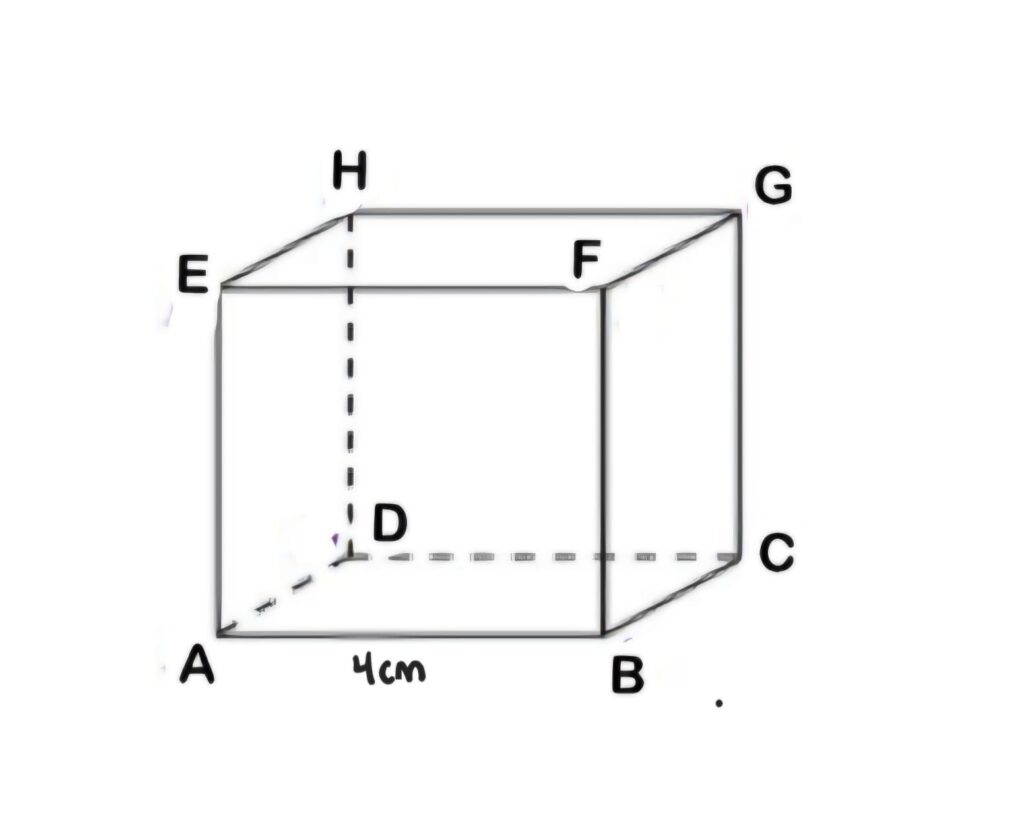
Jika kubus tersebut memiliki panjang sisi 4 cm, tentukan jarak antara titik G dan A!
8. Penyelesaian
Jawaban:
AC = √(AB² + BC²
AC = √(4² + 4²)
AC = √(16 + 16)
AC = √32
AC = 4√2 cm
Langkah 2: Menentukan Panjang AG
AG = √(AC² + GC²)
AG = √((4√2)² + 4²)
AG = √(32 + 16)
AG = √48
AG = 4√3 cm
Jadi, jarak antara titik G dan A adalah 4√3 cm.
